Force and Types of Forces
Introduction to Force
Definition: It is a push or pull upon an object, necessary for performing any work.
➥ It has both magnitude and direction, making it a vector quantity.
Unit: The SI unit of force is the Newton (N) or kg.m/s2.
Dimension = LMT-2
F = ma , where m = mass and a = acceleration
a = v/t , where v = velocity , t = time taken
so, F = mv/t
Examples: Opening doors by pushing or pulling, drawing a drawer.
Effects of Force
- Start a stationary object (e.g., kicking a football).
- Stop a moving object (e.g., applying brakes to a vehicle).
- Change the direction of motion (e.g., steering a bicycle).
- Change the speed of an object (e.g., accelerating or decelerating).
- Alter the shape and size of an object (e.g., hammering metal or stone).
Balanced and Unbalanced Forces
Balanced Forces:→ If the resultant of applied forces is equal to zero, it is called balanced forces.
→ Balanced forces do not cause any change of state of an object.
→ Balanced forces are equal in magnitude and opposite in direction.
→ Balanced forces can change the shape and size of an object.
2. When forces are applied from both sides over a balloon, the size and shape of balloon is changed.
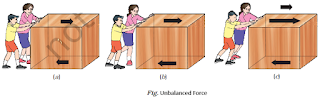
Unbalanced Forces:→ If the resultant of applied forces are greater than zero, the forces are called unbalanced forces.
➥ Net force is the total force on an object, determining its movement; zero net force means no change in motion, while a non-zero net force causes acceleration.
Newton's Laws of Motion
Galileo Galilei: Proposed objects move at constant speed without forces. In reality, external forces like friction always exist.
Newton’s Laws of Motion: Derived from Galileo's ideas, Newton formulated three laws:
Netwon, the father of physics established the laws of motion in his book "principia" in 1687
1. First Law (Law of Inertia)
➥ Object remains in its state of motion unless acted upon by an external force.
Mass and Inertia
Inertia: The property of an object that resists changes in its state of motion.
Inertia is directly proportional to mass. Heavier objects have more inertia.
Examples include difficulty in pushing a heavy box compared to a lighter one.
Momentum
Momentum: The product of an object's mass and velocity. Momentum is denoted by ‘p’.
Momentum Formula: Mass × Velocity (p = m × v) where, p = momentum, m = mass of the object and v = velocity of the object.
Examples illustrating momentum's impact in collisions and accidents.
Unit of Momentum
The units of mass (kg) and velocity (m/s).
SI unit of momentum is kilogram-meter per second (kg·m/s).
Second Law (Law of Acceleration)
➥ Force equals mass times acceleration (F = ma).
Mathematical Expression:
Third Law (Action and Reaction)
➥ For every action, there is an equal and opposite reaction.
(ii) Walking is enabled by 3rd law.
(iii) A gun recoils.
(iv) Rowing of a boat.
When two (or more) bodies act upon one another, their total momentum remains constant (or conserved) provided no external forces are acting.
Initial momentum = Final momentum
Suppose, two objects A and B each of mass m1 and m2 are moving initially with velocities u1 and u2, strike each other after time t and start moving with velocities v1 and v2 respectively.
Now,
Initial momentum of object A = m1 u1
Initial momentum of object B = m2 u2
Final momentum of object A = m1 v1
Final momentum of object B = m2 v2
So,
Rate of change of momentum in A,
F1 = (m1 (v1 - u1))/t ....(i)
Rate of change of momentum in B,
F2 = (m2 (v2 - u2))/t ....(ii)
We know from Newton's Third Law of Motion,
F1 = -F2
So, (m1 (v1 - u1))/t = -(m2 (v2 - u2))/t
⇒ m1 v1 - m1 u1 = -m2 v2 + m2 u2
⇒ m1 u1 + m2 u2 = m1 v1 + m2 v2
Thus, Initial momentum = Final momentum














0 Comments